pollywogs live in treaps

posted on 31 Dec 2019

This post is part of a series on how to achieve sublinear-span chain validation for UTXO systems. It is a follow-up to the post on RTXI.

This example will show how to validate a simple header chain with just two fields and three rules:

  • Each header’s previous field must be the hash of the previous header.
  • Each header’s ancestor field, if it is not null, must point to any earlier header.
  • Each header can only be referenced as an ancestor at most once.

The ‘ancestor’ rule is a bit contrived, but the idea is to show something that is not trivially parallel. It should also remind you of how a transaction output can be consumed by at most one input in a UTXO system.

In a parallel runtime analysis, we assume that there are infinite threads available. We are only interested in the fundamental algorithmic limitations imposed by the structure of the problem.

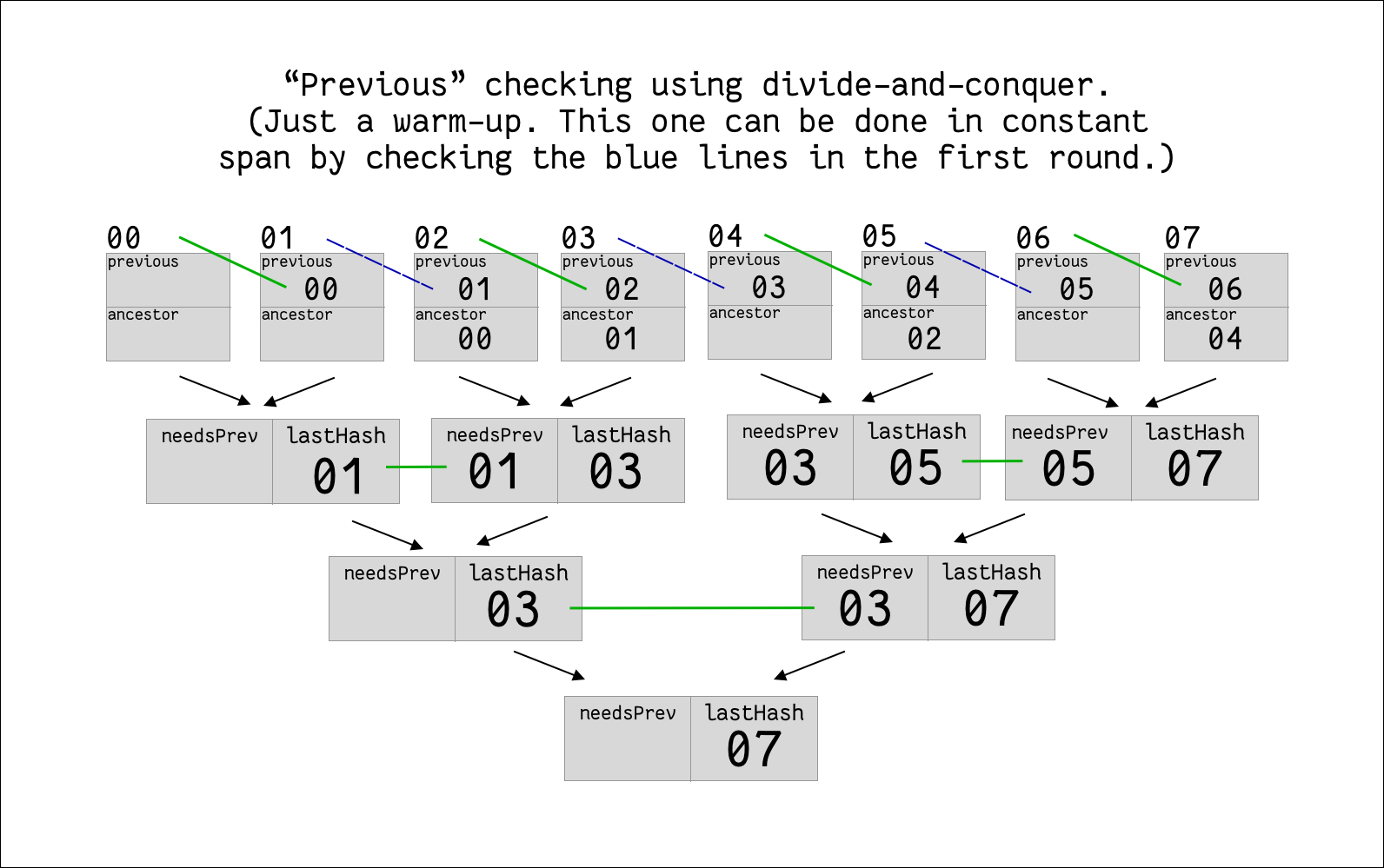
Validating the “previous” field is trivially parallel (O(1) span), as each thread only needs to look at the one previous header. Still, we can structure it as a divide-and-conquer problem to help us get in the right headspace.

We start one thread per transaction, and merge partial results recursively. The intermediate structure we maintain is a (needsPrev, lastHash) pair for each sub-problem. When we merge sub-problems, we ensure that the needsPrev of the “later” half matches the lastHash of the “earlier” half.

diagram showing a contrived log-span algorithm for 'previous' field validation

Now let’s move on to ancestor validation. In each sub-problem, we keep track of “available ancestors” on one side, and “required ancestors” on the other. When we merge two sub-problems, we match any required ancestors from the “later” half with available ancestors from the “earlier” half.

Matching eliminates the required/available ancestor from its respective set. If a required ancestor is not available, validation fails. Validation also fails if there is still a required ancestor left at the end of the process.

Matching ancestors is essentially a pair of set difference operation, which requires O(log^2(n)) expected span. Note that this expectation is with respect to randomization which is a local to the validator, non-deterministic, and independent of the actual values in the set. This is important because otherwise, in a public blockchain system, we would need to assume the adversarial worst-case span and would not be able to treat this expected span as the “real” span.

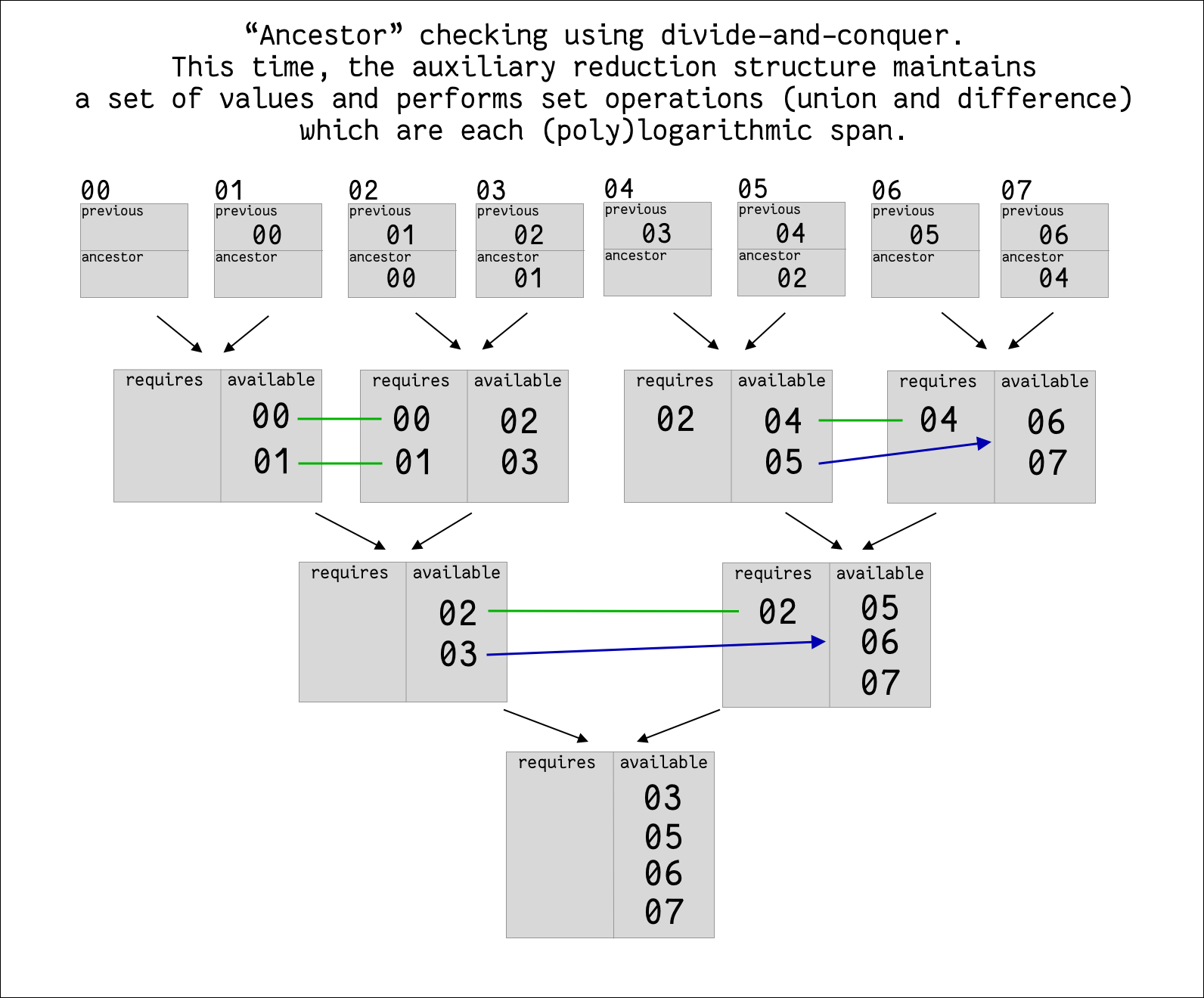
diagram showing a contrived log-span algorithm for 'ancestor' field validation

A simple worst-case bound comes from the fact that each of the O(log(n)) parallel merge steps takes (expected) O(log^2(n)) span, giving O(log^3(n)) total (expected) span. Better bounds might be provable based on the property that matched ancestors are eliminated from the reduction set.

If validation succeeds, we are left with zero required ancestors some number of available ancestors. This “available ancestors” set should remind you of a UTXO set…